제목 : 배달
문제 설명
N개의 마을로 이루어진 나라가 있습니다. 이 나라의 각 마을에는 1부터 N까지의 번호가 각각 하나씩 부여되어 있습니다. 각 마을은 양방향으로 통행할 수 있는 도로로 연결되어 있는데, 서로 다른 마을 간에 이동할 때는 이 도로를 지나야 합니다. 도로를 지날 때 걸리는 시간은 도로별로 다릅니다. 현재 1번 마을에 있는 음식점에서 각 마을로 음식 배달을 하려고 합니다. 각 마을로부터 음식 주문을 받으려고 하는데, N개의 마을 중에서 K 시간 이하로 배달이 가능한 마을에서만 주문을 받으려고 합니다. 다음은 N = 5, K = 3인 경우의 예시입니다.
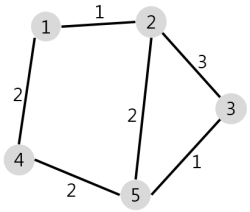
위 그림에서 1번 마을에 있는 음식점은 [1, 2, 4, 5] 번 마을까지는 3 이하의 시간에 배달할 수 있습니다. 그러나 3번 마을까지는 3시간 이내로 배달할 수 있는 경로가 없으므로 3번 마을에서는 주문을 받지 않습니다. 따라서 1번 마을에 있는 음식점이 배달 주문을 받을 수 있는 마을은 4개가 됩니다.
마을의 개수 N, 각 마을을 연결하는 도로의 정보 road, 음식 배달이 가능한 시간 K가 매개변수로 주어질 때, 음식 주문을 받을 수 있는 마을의 개수를 return 하도록 solution 함수를 완성해주세요.
제한사항
- 마을의 개수 N은 1 이상 50 이하의 자연수입니다.
- road의 길이(도로 정보의 개수)는 1 이상 2,000 이하입니다.
- road의 각 원소는 마을을 연결하고 있는 각 도로의 정보를 나타냅니다.
- road는 길이가 3인 배열이며, 순서대로 (a, b, c)를 나타냅니다.
- a, b(1 ≤ a, b ≤ N, a != b)는 도로가 연결하는 두 마을의 번호이며, c(1 ≤ c ≤ 10,000, c는 자연수)는 도로를 지나는데 걸리는 시간입니다.
- 두 마을 a, b를 연결하는 도로는 여러 개가 있을 수 있습니다.
- 한 도로의 정보가 여러 번 중복해서 주어지지 않습니다.
- K는 음식 배달이 가능한 시간을 나타내며, 1 이상 500,000 이하입니다.
- 임의의 두 마을간에 항상 이동 가능한 경로가 존재합니다.
- 1번 마을에 있는 음식점이 K 이하의 시간에 배달이 가능한 마을의 개수를 return 하면 됩니다.
입출력 예
| N | road | K | result |
| 5 | [[1,2,1],[2,3,3],[5,2,2],[1,4,2],[5,3,1],[5,4,2]] | 3 | 4 |
| 6 | [[1,2,1],[1,3,2],[2,3,2],[3,4,3],[3,5,2],[3,5,3],[5,6,1]] | 4 | 4 |
입출력 예 설명
입출력 예 #1
문제의 예시와 같습니다.
입출력 예 #2
주어진 마을과 도로의 모양은 아래 그림과 같습니다.

1번 마을에서 배달에 4시간 이하가 걸리는 마을은 [1, 2, 3, 5] 4개이므로 4를 return 합니다.
분석
다익스트라(Dijkstara's algorithm)을 이용하는 문제이다.
구현
#define INF 987654321;
using namespace std;
int dist[51];
vector<pair<int, int>> node[51];
int result = 51;
void dijkstra(int start)
{
dist[start] = 0;
priority_queue<pair<int, int>> pq;
pq.push({ dist[start],start });
while (!pq.empty())
{
int cur = pq.top().second;
int distance = pq.top().first * -1;
pq.pop();
if (dist[cur] < distance) continue;
for (size_t i = 0; i < node[cur].size(); i++)
{
int next = node[cur][i].first;
int nextDistance = distance + node[cur][i].second;
if (nextDistance < dist[next])
{
dist[next] = nextDistance;
pq.push({ nextDistance * -1, next });
}
}
}
}
int solution(int N, vector<vector<int> > road, int K)
{
int answer = 1;
for (size_t i = 1; i <= N; i++)
{
dist[i] = INF;
}
for (size_t i = 0; i < road.size(); i++)
{
node[road[i][0]].push_back({ road[i][1],road[i][2] });
node[road[i][1]].push_back({ road[i][0],road[i][2] });
}
dijkstra(1);
for (size_t i = 2; i <= N; i++)
{
if (dist[i] <= K) answer++;
}
return answer;
}
int main()
{
vector<vector<int>> road = { {1,2,1},{1,3,2},{2,3,2},{3,4,3},{3,5,2},{3,5,3},{5,6,1} };
cout << solution(6, road, 4); // 4
return 0;
}'알고리즘 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스 C++] 방문 길이 (0) | 2021.03.14 |
|---|---|
| [프로그래머스 C++] 게임 맵 최단거리 (0) | 2021.03.07 |
| [프로그래머스 C++] 2018 카카오 3차 n진수 게임 (210) | 2021.03.03 |
| [프로그래머스 C++] 2018 카카오 3차 파일명 정렬 (0) | 2021.03.01 |
| [프로그래머스 C++] 2018 카카오 3차 압축 (0) | 2021.02.28 |
