알고리즘/알고리즘 문제 해결 전략

[C++] 이진 트리 + 힙, 트립
트립 (treap) 보통 STL에서 제공하는 이진 검색 트리는 대부분 X보다 작은 원소의 수를 계산하거나, k번쩨 원소를 찾는 연산을 지원하지 않는다. 따라서 필요할 때는 직접 군형 잡힌 이진 트리를 구현해야 하는데, 이게 쉽지 않은 작업이다. (속도나 효율도 별로다..) 그렇기에 필요한 경우 간단하게 구현이 가능한 treap을 사용한다. 정의 트립은 입력이 특정 순서로 주어질 때 성능이 떨어진다는 이진 검색 트리의 단점을 해결하기 위해 고안된 이진 검색 트리이다. 원리는 트리의 형태가 원소들의 추가 순서에 따라 결정되지 않고, 난수에 의해 임의대로 결정된다. 그렇기에 노드가 추가되거나 삭제되더라도 트리 높이의 기대치는 항상 일정하다. 이와 같은 속성을 만족시키려면 두가지 조건이 성립돼야 한다. 1. 이..

알고스팟 - 너드인가, 너드가 아닌가? 2
문제 : 너드인가, 너드가 아닌가? 2 (난이도 : 中) 분석 너드인가를 판단하는 매게 변수가 두 가지로 주어졌다. 너드가 아닌 경우는 두 가지 매게 변수 모두 다른 포인트보다 작을 경우이다. 이런 유형을 다룰 땐 주어진 데이터를 좌표평면 위에 그리면 쉽게 해결할 수 있다. 이렇게 좌표 평면위에 두면 할 일이 간단해진다. 지배하는 점들의 규칙을 살펴보면 x좌표가 커질수록 y좌표가 작아짐을 알 수 있다. 따라서 새로운 데이터를 추가할 때 기존 지배하는 점의 가장 오른쪽 x좌표보다 큰 지, 아니라면 y 값이 큰 지를 판단하면 된다. STL의 map을 이용하기 좋은 문제 상황이다. 구현 map coords; // 새로운 점 (x, y)가 기존의 다른 점들에 지배당하는지 확인 bool isDominated(in..
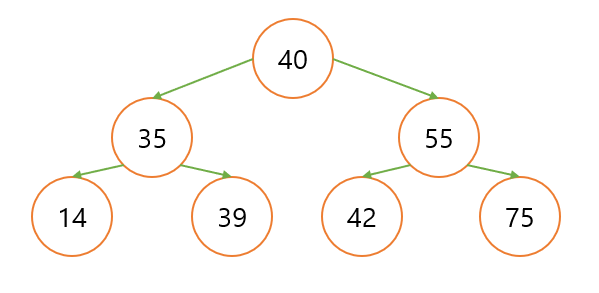
이진 탐색 트리(Binary Search Tree)
이진 탐색 트리 : BST 정의 이진 탐색 트리 정의에 앞서 이진 트리(binary tree)를 정의하자. 이진 트리란 왼쪽, 오른쪽 최대 두 개의 자식 노드를 가질 수 있는 트리를 의미한다. 이때 자식 노드들은 배열이 아닌 포인터로 left와 right를 담는 객체로 구현한다. 단, left 노드 값은 부모 노드보다 작은 값이고 right 노드 값은 부모 노드보다 큰 값이어야 한다. 이진 탐색 트리는 이런 이진 트리 구조에 이진 탐색(binary search)의 아이디어를 가져와 만든 트리이다. 이진 탐색이란 N개 원소 중 원하는 값을 찾을 때, 매번 탐색 값을 절반씩 줄여가며 탐색하는 것을 의미한다. 이렇게 되면 O(lgN) 시간에 원하는 값을 찾을 수 있다. 순회 및 검색 순회 및 검색을 할 때 이..

[알고스팟] - 요새
문제 : 요새 (난이도 : 中) 분석 주어진 데이터를 트리 형태로 가공하면 쉽게 답을 구할 수 있다. 트리 형태에서 최장 길이는 다음 중 긴 길이에 해당된다. 1. 트리의 높이 2. 잎-잎 길이 입력 데이터 중 첫 번째 데이터는 성 외곽이므로 트리의 root로 설정하고, 나머지 tree를 구성하면 된다. 구현 struct TreeNode { vector children; }; // leaf to leaf len int longest; // root를 루트로하는 subtree의 높이를 반환. int height(TreeNode* root) { vector heights; for (size_t i = 0; i children.size(); i++) { heights.push_back(heigh..

알고스팟 - 트리 순회 순서 변경
문제 : 트리 순회 순서 변경 (난이도 : 下) 분석 전위 순회 데이터를 통해 root 값을 확정적으로 알 수 있다. (preorder[0]) 중위 순회 데이터를 통해 왼쪽 트리와 오른쪽 트리의 개수 파악이 가능하다. 이를 적절히 조합하면 후위 순회 데이터를 추출할 수 있다. 구현 ※ std::find() 함수의 활용과 printPostOrder() 호출 순서를 눈여겨보자. vector slice(const vector& v, int a, int b) { return vector(v.begin() + a, v.begin() + b); } void printPostOrder(const vector& preorder, const vector& inorder) { const int N = preorder.si..

알고스팟 - 외계 신호 분석
문제 : 외계 신호 분석 (난이도 : 中) 분석 이 문제의 핵심은 입력단의 크기이다. 모든 입력단을 처리하기에는 너무 큰 것을 알 수 있다. 따라서 이 문제는 온라인 알고리즘(online algorithm)을 사용해야 한다. 온라인 알고리즘(online algorithm): 전체 입력이 한 번에 주어지지 않아도 계산을 할 수 있는 알고리즘을 말한다. 예를 들어 삽입 정렬은 새 원소를 이전의 정렬된 목록에 끼워 넣는 방법으로 동작하는데, 처음에 모든 원소가 주어지지 않아도 정렬을 시작할 수 있다. 오프라인 알고리즘(ofline algorithm): 반면 선택 정렬은 남아 있는 모든 원소 중에서 최소의 원소를 찾아서 맨 앞에 옮기는 방식으로 동작하므로, 모든 원소를 알고 있어야 한다. 일단 입력단의 크기를 ..

스택 - 1. 짝이 맞지 않은 괄호
문제 : 짝이 맞지 않은 괄호 (난이도 : 下) 분석 Stack의 구조인 LIFO(Last In First Out)를 안다면 쉽게 접근할 수 있는 문제이다. 짝이 맞는지 확인하는 함수 wellMatched()에서 짝을 맞추는 과정을 유의 깊게 봐보자. (주석 참조) 구현 bool wellMatched(const string& input) { // opening과 closing의 문자 순서를 유심히 보자. // idx로 짝을 맞추기에 같은 순서로 선언됐다. const string opening("({["), closing(")}]"); stack openStack; for (int i = 0; i < input.size(); i++) { // find() 함수는 일치하는 idx를 반환한다. // 만약 일치..

연결 리스트 - 조세푸스 문제
문제 : 조세푸스 문제 (난이도 : 下) 분석 문제 상황이 원형 리스트 상태이다. STL에선 원형 리스트를 지원하지 않으므로 약간의 변형을 통해 구현하면 쉽게 문제를 해결할 수 있다. 구현 void josephus(int n, int k) { list survivors; for (int i = 1; i 2) { // earse() 지운 원소의 다음 원소를 반환 kill = survivors.erase(kill); if (kill == survivors.end()) kill = survivors.begin(); n--; // k-1 번 다음 사람으로 옮긴다. for (int i = 0; i < k - 1; i++) { kill++; if (kill == survivors.end()) kill = survi..