문제 : 울타리 잘라내기 (난이도 中)
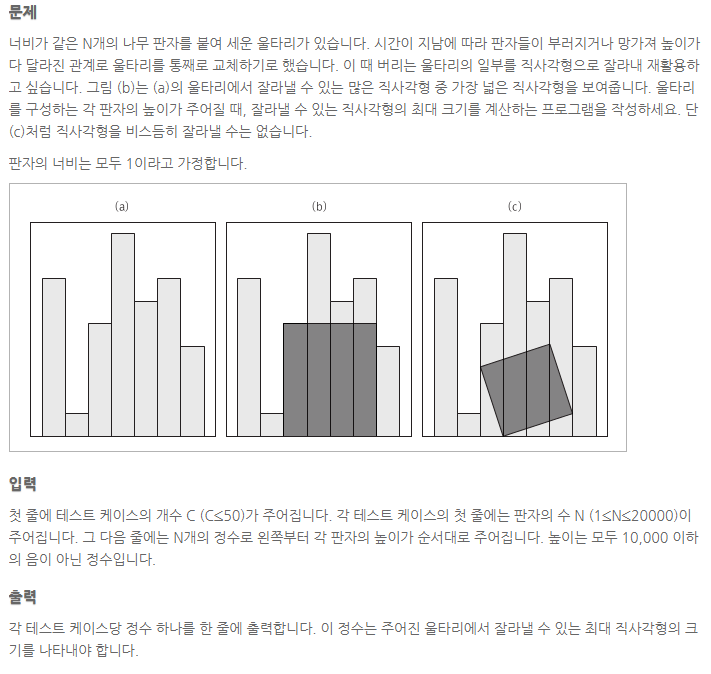
분석
이 문제를 보면 무식하게 풀기(Brute force)를 어느 정도 공부했던 사람이면 쉽게 이중 for문으로 해결하려 할 것이다.
int makeMax(const vector<int>& h)
{
int ret = 0;
for (int left = 0; left < h.size(); left++)
{
int minHeight = h[left];
for (int right = left; right < h.size(); right++)
{
int lenght = right - left + 1;
minHeight = min(minHeight, h[right]);
ret = max(ret, lenght*minHeight);
}
}
return ret;
}
그러나 시간 복잡도를 보면 이중 for문이기에 O(n^2) 이 나오는데, 입력의 최대 크기가 20,000 임을 보면 위 방식으로 이 문제를 풀기엔 다소 시간이 걸린다는 것을 알 수 있다.
분할 정복 설계
가장 큰 직사각형 기준으로 입력 전체를 덮을때까지 확장해 가며 가장 큰 넓이를 확인하면 된다.
말로 이해하는 것보다 코드를 보며 직접 이해하는 것이 빠를 것이다.
구현
int bruteforce(const vector<int>& h)
{
int ret = 0;
for (int left = 0; left < h.size(); left++)
{
int minHeight = h[left];
for (int right = left; right < h.size(); right++)
{
int lenght = right - left + 1;
minHeight = min(minHeight, h[right]);
ret = max(ret, lenght*minHeight);
}
}
return ret;
}
vector<int> h;
//h[left, right] 구간에서 찾을 수 있는 가장 큰 사각형의 넓이를 반환한다.
int solve(int left, int right)
{
//base case : only one fence
if (left == right) return h[left];
//[left, mid], [mid + 1, right] 두 구간으로 문제를 분할한다.
int mid = (left + right) / 2;
//각개격파; 분할 후 가장 큰 사각형을 찾는다.
int ret = max(solve(left, mid), solve(mid + 1, right));
//두 부분에 걸치는 사각형 중 가장 큰 것을 찾는다.
int lo = mid, hi = mid + 1;
int height = min(h[lo], h[hi]);
//[mid, mid+1]가 만드는 사각형을 고려한다.
ret = max(ret, height * 2);
while (left < lo || hi < right)
{
//항상 높이가 더 높은 쪽으로 확장해 나간다.
if (hi < right && (lo == left || h[lo - 1] < h[hi + 1]))
{
hi++;
height = min(height, h[hi]);
}
else
{
lo--;
height = min(height, h[lo]);
}
ret = max(ret, height * (hi - lo + 1));
}
return ret;
}
int main()
{
time_t start, end;
double result;
int ans;
//1~1000
int n_num[1000] = {};
for (int i = 0; i < 1000; i++)
{
n_num[i] = i + 1;
}
int n;
cin >> n;
//난수 값 넣기
for (int i = 0; i < n; i++)
{
srand(i);
int idx = rand() % 1000;
h.push_back(n_num[idx]);
}
for (int i = 0; i < n; i++)
{
cout << h[i] << ' ';
}putchar('\n');
start = clock();
ans = solve(0, h.size() - 1);
end = clock();
result = (double)(end - start);
cout << ans << ", 분할 정복 소요 시간 : " << result << "ms" << '\n';
start = clock();
ans = bruteforce(h);
end = clock();
result = (double)(end - start);
cout << ans << ", brute forte 소요 시간 : " << result << "ms" << '\n';
return 0;
}
solve() 함수에서 핵심은 가장 큰 직사각형의 넓이를 기준으로 확장 높이가 큰 쪽으로 항상 확장해가며, 값을 비교하는 것이다.
소요 시간 비교

solve() 함수의 시간 복잡도를 계산해보면, O(nlgn) 이다.
실제로 비교하게 되면 차이가 극명하게 나는 것을 볼 수 있다.
'알고리즘 > 알고리즘 문제 해결 전략' 카테고리의 다른 글
| 동적 계획법 & 메모이제이션 (0) | 2020.11.26 |
|---|---|
| 분할정복 - 3. 팬미팅 (387) | 2020.11.22 |
| 분할 정복 - 1. 쿼드 트리 뒤집기 (0) | 2020.11.16 |
| 분할 정복 - 카라츠바 알고리즘 (1) | 2020.11.14 |
| 분할 정복 (Divide & Conquer) (0) | 2020.11.13 |
